Hex to Binary: A JS Canvas Game
Back in my high school Computer Science classes, there was a game our teacher showed us to help us learn about binary and hexadecimal number systems. The game involved converting 2-digit hexadecimal numbers to 8-bit binary sequences. This way, we could learn the relationship between binary, denary and hexadecimal, and how to convert numbers between them. I haven’t been able to find out what that game was called, but when recovering some old files, I found this JavaScript clone I made of that very game back in high school.
Here’s some info on how to convert between hexadecimal and binary.
A brief explanation of these number systems
To begin, binary works in powers of two, with each successive bit giving us double the number of permutations. Here is a small table to illustrate this:
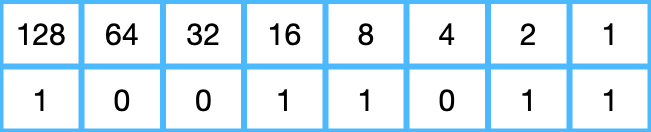
Summing the place values of columns that contain a 1, we get 128 + 16 + 8 + 2 + 1 = 155. So 10011011 is equivalent to 155 in denary.
To convert a 2-digit hexadecimal number into an 8-bit binary sequence, we need to convert each hex digit to 4 bits (a nibble). Let’s try converting 5A to binary. Using the above table as a reference, we can see that to represent 5, we’ll need a 4 and a 1. So 5 becomes 101 in binary, or 0101 using 4 bits. The hex digit A is 10 in denary, so to represent this in binary, we’ll need an 8 and a 2. So 10 becomes 1010 in binary. Putting those two together, we get 01011010, or 5A in hexadecimal.
The hexadecimal to binary game
The game rules are simple: as the hexadecimal digits enter the screen from the left, you have to find each number’s binary equivalent before it exits the end of the screen.
As I mentioned, I wrote this back in high school and never really got around to completing it, but it’s still playable. Give it a try and see how fast you can get at making these conversions!